KMP 详解

发表于 分类于 阅读次数： Waline：
字符串子串问题的极致复杂度！

引入

什么是 KMP？

KMP 是一种 \(O(n)\) 求解一个字符串 \(t\) （模式串）在另一个字符串 \(s\) （主串）中 所有 出现的地方和总次数。

KMP 有什么用？

可以解决很多关于子串的问题。

以下使用 \(s[l .. r]\) 表示 \(s_ls_{l + 1}\cdots s_r\)。

思路

暴力算法

首先考虑暴力算法：

枚举 \(i \in [1, n]\)，比较 \(t[i .. i + len(m) - 1]\) 和 \(s\)。
时间复杂度 \(O(n^2)\)。

过程：

那么为什么暴力这么慢呢？
问题出在两个地方：

  1. 每一个位置都要比较
  2. 字符串需要 \(O(n)\) 比较

第二个基本上没法优化了（因为字符串比较真的需要 \(O(n)\)），但第一个可以优化。
我们只需要不让每一个位置都需要比较就好了。

于是我们就得到 KMP 的核心思想。

KMP 思想

我们在暴力匹配时除了匹配成功与失败，还有 别的有用信息 吗？
答案是有的。

除了没有匹配成功以外，我们还可以得到 有多少个字符的前缀是可以匹配的。

例如：

那么知道了这些信息有什么用呢？
我们可以 将一些情况排除，也就是跳过从某些位置开始匹配的步骤！

具体的：

再看一个例子：

当我们发现已知的字符串可以匹配主串前几位时，就可以计算出下一步直接移动到哪里，跳过一些情况。
这就是 \(next\) 数组！

next 数组

next 定义

\(next(i)\) 表示在 \(t[1 .. i]\) 中，满足 \(t[1 .. x] = t[i - x + 1 .. i]\) 且 \(x < i\) 的最大的 \(x\)。（这里是对模式串做匹配哦）

\(s\) 是主串，\(t\) 是模式串。

next 用法

求出了 next 数组如何求出答案呢？

考虑一个字符串：

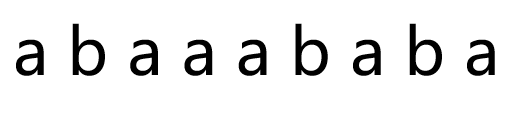
那么它的 next 如下：

这个 next 有什么用呢？看下图：

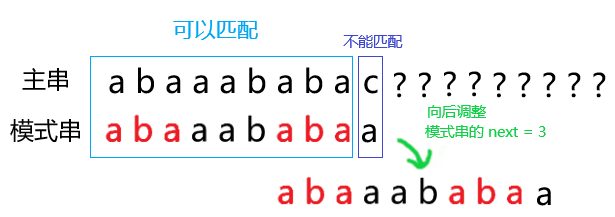
我们发现，每次向后移动是将 能匹配上的字符串 的 长度为 \(next(i)\) 的前缀后缀 对齐。
也即：如果模式串 \(t\) 的前 \(i\) 个字符能匹配上，那么将模式串向后移动 \(i - next(i)\) 个字符，匹配下标从 \(i - next(i)\) 移动到 \(next(i)\)。（见下图）

next 求法

采用 DP 思想：现在已经求出了 \(next(1 .. i - 1)\)，如何求 \(next(i)\)？

对于下面字符串：

第一种情况，向后一个字符（图中蓝色）也相同，直接转移即可。

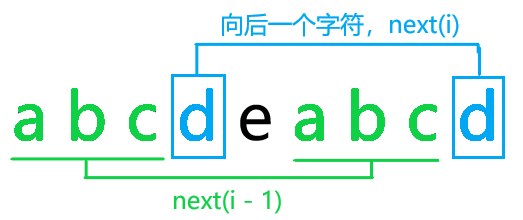
第二种情况，向后一个字符（图中红色）不同。

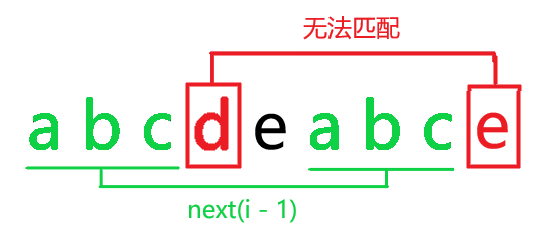
怎么办呢？
这时就要退而求其次，也就是说我们要取一个比 \(next(i - 1)\) 更小一点的 \(x\) 使得 \(t[1 .. x] = t[i - x + 1 .. i]\)。
直接上结论：取 \(x = next(next(i - 1))\)

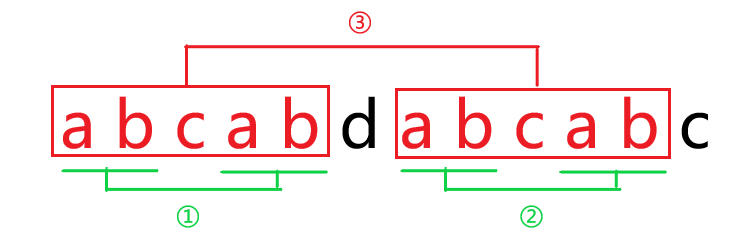
原因：
由 \(next(i - 1)\) （红色）得③处相等，而由 \(next(next(i - 1))\) （绿色）得①处相等。
①和③放在一起推得①②的四个字符串都相等，所以得到 \(t[1 .. x] = t[i - x + 1 .. i]\)。

复杂度

容易发现 \(j\) 的增量不超过 \(n\) （见代码），所以它的减少量也不超过 \(n\)，所以总复杂度 \(O(n)\)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void kmp(const char *s, const char *t, vector<int> &ans) { // s, t 下标从 1 开始
    n = strlen(s + 1), m = strlen(t + 1);
    next[1] = 0; // 如果下标从 0 开始，那么这里应该是 next[0] = -1
    for(int i = 2, j = 0; i <= m; i++) {
        while(j && t[j + 1] != t[i]) j = next[j];
        if(t[j + 1] == t[i]) j++;
        next[i] = j;
    }
    for(int i = 1, j = 0; i <= n; i++) {
        while(j && t[j + 1] != s[i]) j = next[j];
        if(t[j + 1] == s[i]) j++;
        if(j == m) {
            ans.push_back(i - m + 1);
            j = next[j]; // 匹配结束之后也要继续匹配
        }
    }
}

例题

洛谷 P3375

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <cstdio>
#include <cstring>

const int N = 1e6 + 5;

char s[N], t[N];
int nxt[N];

int n, m;

int main() {
	std::scanf("%s%s", s + 1, t + 1);
	n = std::strlen(s + 1), m = std::strlen(t + 1);
	nxt[0] = -1;
	for(int i = 1; i <= m; i++) {
		int j = nxt[i - 1];
		while(t[j + 1] != t[i] && j != -1) j = nxt[j];
		nxt[i] = j + 1;
	}
	int j = 0;
	for(int i = 1; i <= n; i++) {
		while(j && t[j + 1] != s[i]) j = nxt[j];
		if(t[j + 1] == s[i]) j++;
		if(j == m) {
			std::printf("%d\n", i - m + 1);
			j = nxt[j];
		}
	}
	for(int i = 1; i <= m; i++) std::printf("%d ", nxt[i]);
	return 0;
}