快速傅里叶变换（FFT）及快速数论变换（NTT）详解

发表于 分类于 阅读次数： Waline：
换一条看起来更长的路走，有时会带来意想不到的惊喜！

前置知识

复数
单位根（下面讲）
多项式（下面讲）

单位根

前置知识：复数

在复平面上，所有与原点距离为 \(1\) 的点组成单位圆。
由于两个复数相乘的法则（辐角相加，模长相乘），在单位圆上的两个复数相乘还是在单位圆上（模长都是 \(1\)），且辐角为这两个复数相加。
所以对于 \(x^n=1\) 这个方程来说，它的解在单位圆上，且辐角为 \(\frac{360}{n}\) 的倍数，显然这样的复数有 \(n\) 个，我们把这样的 \(n\) 个复数叫做 \(n\) 次单位根，并将其中辐角最小的（\(1\) 除外）记作 \(\omega_n\)。
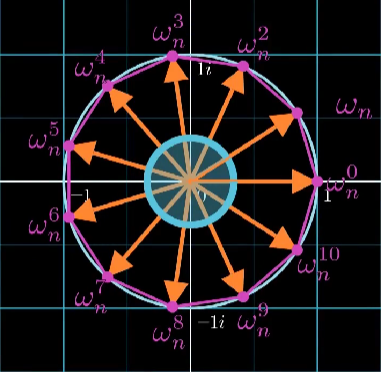
所有 \(\omega_n^i\) 都是 \(n\) 次单位根。

上图就是 \(11\) 次单位根 在复平面上的表示。

单位根有三个引理：（证明显然）

  1. 消去引理：\(\omega_{kn}^{km} = \omega_n^m\)
  2. 折半引理：\(\left(\omega_{n}^{k+\frac{n}{2}}\right)^2=\omega_{n}^{2k}=\omega_{\frac{n}{2}}^k\)
  3. 求和引理：\(\sum_{i=0}^{n-1} \left(\omega_n^k\right)^i = 0\)

在 FFT 中，我们只需要用前两个。

多项式

这里我们讨论的多项式是只有一个变量 \(x\) 的多项式，即 \(F(x) = \sum_{i=0}^n a_i x^i\)。

多项式有两种表示方法：（设多项式有 \(n + 1\) 项）

  1. 系数表示，即将多项式表示成：\([a_0, a_2, \cdots, a_n]\)，其中 \(a_i\) 为 \(x^i\) 项的系数
  2. 点值表示，即将多项式表示成：\([(v_0, F(v_0)), (v_1, F(v_1)), \cdots, (v_n, F(v_n))]\)，即将 \(n + 1\) 个不同的值 \(v_i\) 带入多项式得到 \(F(v_i)\)，然后用这 \(n + 1\) 个二元组唯一确定一个多项式。（不考虑那种无用点值之类的东西）

容易发现，对于两个多项式 \(F(x)\) 和 \(G(x)\)，设 \(H(x) = F(x) \times G(x)\)，如果有 \(F\) 和 \(G\) 的点值表示，那么 \(H\) 的点值表示也可以很快算出来：\(H(v_i) = F(v_i) \times G(v_i)\)。

所以，FFT 要做的事就是将系数表示转换成点值表示（及其逆过程，这个后面再说）。

FFT

几个概念

  1. 离散傅里叶变换（Discrete Fourier Transform，DFT），即 将系数表示转换成点值表示，其中 \(v_i = \omega_n^i\)。
  2. 快速傅里叶变换（即 快速（离散）傅里叶变换，Fast (Discrete) Fourier Transform，FFT），即快速做 DFT。

思路

从这里开始，我们将 \(n\) 定为多项式的项数，而不是多项式的次数。

FFT 可以（且必须）直接计算 \(2^k\) 个点值，所以我们将 \(n\) 取到比它大（或等于它）的最小的 \(2\) 的幂次。（\(n \gets 2^k\)）

设多项式为 \(F(x) = \sum_{i=0}^{n - 1} a_i x^i\)，并且令点值表示法为 \([(v_0, y_0), (v_1, y_1), \cdots, (v_{n-1}, y_{n-1})]\)。
容易发现 \(y_i = \sum_{j=0}^n a_j (v_i)^j = \sum_{j=0}^n a_j v_i^j\)。

我们首先将 \(F(x)\) 的系数 \(A = [a_0, a_1, \cdots, a_{n - 1}]\) 按奇偶分为 \(A^{[0]}\) 和 \(A^{[1]}\)，即：
\(A^{[0]} = [a_0, a_2, \cdots, a_{n - 2}]\), \(A^{[1]} = [a_1, a_3, \cdots, a_{n - 1}]\)。

那么我们会发现 \(F(x) = F^{[0]}(x^2) + xF^{[1]}(x^2)\)，读者自证不难。
所以我们就有了一个分治想法：用 \(F^{[0]}\) 和 \(F^{[1]}\) 的点值表示来算出 \(F\) 的点值表示。

但是这里会有一个问题：\(F^{[0]}\) 和 \(F^{[1]}\) 的点值表示都只有 \(\frac n2\) 个，所以合并后也只有 \(\frac n2\) 个。
所以我们还需要用 \(F^{[0]}\) 和 \(F^{[1]}\) 的 \(\frac n2\) 个点值来求出 \(F\) 的后 \(\frac n2\) 个点值。

这怎么办呢？随便取 \((v_i, y_i)\) 的值肯定是无法做到的，我们要取一些有特殊性质的值。现在就要用到我们之前说的单位根了。

我们取 \(v_i = \omega_n^i\)，这有什么用呢？我们代两个值进去看看：（记 \(k' = k + \frac n2\)）

\[ \begin{aligned} F(v_k) = F(\omega_n^k) = F^{[0]}((\omega_n^k)^2) + \omega_n^k F^{[1]}((\omega_n^k)^2) = F^{[0]}(\omega_{\frac n2}^k) + \omega_n^k F^{[1]}(\omega_{\frac n2}^k)\\ F(v_{k'}) = F(\omega_n^{k'}) = F^{[0]}((\omega_n^{k'})^2) + \omega_n^{k'} F^{[1]}((\omega_n^{k'})^2) = F^{[0]}(\omega_{\frac n2}^k) - \omega_n^k F^{[1]}(\omega_{\frac n2}^k) \end{aligned} \]

所以我们只需要用 \(F^{[0]}\) 和 \(F^{[1]}\) 点值表示就可以直接求出 \(F\) 的点值表示啦。

然后怎么办呢？对于 \(n = 1\) 的情况，\(F(x) = A_0 x\)，又由于 \(n = 1\)，所以 \(x_0 = 1\)，那么 \(F(x)\) 的点值表示就是 \(A_0\) 啦。

非递归写法

由于 FFT 非常的常用，常数也很大，所以我们需要一定的卡常技巧。为了学习隔壁的 zkw 线段树我们发明出了 FFT 的非递归写法。

首先我们发现，只要求出所有 \(n = 1\) 时的点值表示，其它的就可以轻松地用循环求出（把递归树画出来，用循环模拟过程。因为 \(n\) 是 2 的幂次，所以很好模拟）。

所以现在我们只需要求出 \(n = 1\) 时的点值表示。考虑一个递归过程：（每次将上面一行 \(A\) 分成两个 \(A^{[0]}\) 和 \(A^{[1]}\)，将两个数组用 | 隔开）

1
2
3
4
F(8): a[0]   a[1]   a[2]   a[3]   a[4]   a[5]   a[6]   a[7]
F(4): a[0]   a[2]   a[4]   a[6] | a[1]   a[3]   a[5]   a[7]
F(2): a[0]   a[4] | a[2]   a[6] | a[1]   a[5] | a[3]   a[7]
F(1): a[0] | a[4] | a[2] | a[6] | a[1] | a[5] | a[3] | a[7]

我们再来看最后一行的下标，这次我们用二进制表示出来：（上面是十进制，下面是二进制）

1
2
 0   4   2   6   1   5   3   7
000 100 010 110 001 101 011 111

这个二进制有什么规律呢？我们将每个二进制倒过来并转成十进制看看：（上面是倒过来的二进制，下面是十进制）

1
2
000 001 010 011 100 101 110 111
 0   1   2   3   4   5   6   7

现在规律已经很明显了。我们要求的数在二进制意义下倒过来是顺序排列的，我们把这种序列叫做 逆二进制序。

那么现在我们就解决了非递归版的 FFT。

代码在最后面。

逆 FFT（IFFT）

我们再回到之前的公式：\(y_i = \sum_{j=0}^n a_j \omega_n^{ij}\)。
我们把它写成矩阵：\(\textbf{y} = \textbf{V}_n \times \textbf{a}\)，其中 \(\left(\textbf{V}_n\right)_{i,j} = \omega_n^{ij}\)。
所以 \(\textbf{a} = \textbf{V}_n^{-1} \textbf{y}\)，其中 \(\textbf{V}_n^{-1}\) 是 \(\textbf{V}\) 的逆矩阵。
通过某些我不会的方法算出来：\(\left(\textbf{V}_n^{-1}\right)_{i,j} = \frac{\omega_n^{-ij}}{n}\)。
然后就用 FFT 的方法，改一下公式就好了。

代码在最后面。

NTT

FFT 的优势很多，但是缺陷也很明显：需要用 double，所以会有精度问题，而且不能取模。

那么有没有其它的东西可以支持取模且没有精度问题呢？当然是有的，这就是快速数论变换（NTT，Number Theoretic Transform）。

这里的 NTT 解决的是模数为 \(998244353\) 的做法。如果是其它的模数，需要使用下面的 任意模数 NTT。

首先观察一下 \(998244353\) 的性质：（数论不懂的可以看看我 这篇 博客）

  • 它是一个质数。
  • \(\varphi(998244353) = 998244352 = 2^{23} \times 7 \times 17\)
  • 它有 原根，其中一个是 \(3\)。

什么是原根？

对于两个数 \(a\) 和 \(m\)，如果 \(\gcd(a, m) = 1\)，那么我们有 \(a^{\varphi(m)} \equiv 1 \pmod m\)（欧拉定理）。

如果对于任意 \(0 \le n < \varphi(m)\)，满足 \(a^n \not \equiv 1 \pmod m\)，那么我们称 \(a\) 是 \(m\) 的原根。

我们回到 FFT 上来。当时我们为什么要令 \(x_i = \omega_n^i\) 呢？因为它满足一下几条性质：

  • \(\{\omega_n^i\} (0 \le i < n)\) 互不相同
  • \(\omega_{km}^{kn} = \omega_m^n\)
  • \(\left(\omega_{n}^{k+\frac{n}{2}}\right)^2=\omega_{n}^{2k}=\omega_{\frac{n}{2}}^k\)

那么我们用原根是否也能做到这几条性质呢？答案是可以。

记原根为 \(g\)（模数为 \(998244353\) 时 \(g=3\)），那么我们令 \(g_n = g^{p - 1 \over n}\)，并令 \(x_i = g_n^i\)。

那么我们可以证明这几条性质：（第一条上面 OI-Wiki 的链接里有，我 不会证 就不证了）

  • \(g_{km}^{kn} = g^{\frac{km(p - 1)}{kn}} = g^{\frac{m(p - 1)}{n}} = g_m^n\)
  • \(\left(g_n^{k + \frac n2}\right)^2 = g_n^{2k+n} = g_n^{2k} = g_{\frac n2}^k\)

那么我们就完美解决了所有性质，把 FFT 的板子套上去，换成 NTT 的公式就好了。

这时候有小可爱可能就会问了：你这个 \(g^{\frac{p - 1}{n}}\) 中指数 \(\frac{p - 1}{n}\) 有没有可能不是整数啊？

这就要用到上面的质因数分解了：\(p - 1 = 998244352 = 2^{23} \times 7 \times 17\)，又因为前面我们把 \(n\) 调整为 \(2\) 的幂次了，所以当 \(n \le 2^{23} = 8388608 \approx 8.3 \times 10^6\) 时都是够用的啦。

另外，这种方法不止适用于 \(998244353\)，还有 \(469762049\) 和 \(1004535809\)。（它们的原根都是 \(3\) 哦）

另外一些数也可以用这种方法，参见 原根表。

代码在最后面。

任意模数 NTT（MTT）

如果模数不是上面的，或者在输入中给定，又怎么办呢？

这时候就需要 任意模数 NTT（any Module NTT）了。

对于任意模数，我们无法得到上面的性质了。怎么办呢？我们可以自己取模数！

具体地，我们取一些模数 \(p_1, p_2, \cdots p_k\) 使得答案多项式的系数在 取模之前 不会超过 \(\prod p_i\)。一般来说取 \(3\) 个质数（\(998244353\)，\(469762049\)，\(1004535809\)）就够了。

然后我们先算出答案对每个 \(p_i\) 取模的结果，利用 CRT 就可以求得答案对 \(\prod p_i\) 取模的结果。又因为答案小于 \(\prod p_i\)，所以这个结果就是答案。（可以在 CRT 的过程中就对原题模数取模，这样就不会爆 long long）然后将这个答案对题目中的模数取一次模就好了。

例题：洛谷 P4245

代码在最后面。

代码

都是非递归版的。

FFT 和 IFFT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cmath>
#include <algorithm>
const int N = /* ... */ + 5; // 2 * (n + m)
const double PI = acos(-1);
struct Complex {
	double x, y;
	Complex(double x_ = 0, double y_ = 0) : x(x_), y(y_) {}
};
Complex operator+(const Complex &a, const Complex &b) { return Complex(a.x + b.x, a.y + b.y); }
Complex operator-(const Complex &a, const Complex &b) { return Complex(a.x - b.x, a.y - b.y); }
Complex operator*(const Complex &a, const Complex &b) { return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }
struct FFT {
	int rev[N];
	int limit;
	int init(int mx) {
		int w = 0;
		limit = 1;
		while(limit <= mx) limit <<= 1, w++; // w = log2(limit)
		for(int i = 0; i < limit; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (w - 1));
		return limit;
	}
	void trans(Complex *a, int type) { // type = 1 / -1
		for(int i = 0; i < limit; i++) if(i < rev[i]) std::swap(a[i], a[rev[i]]);
		for(int i = 1; i < limit; i <<= 1) {
			Complex wn = Complex(cos(PI / i), type * sin(PI / i));
			for(int j = 0; j < limit; j += (i << 1)) {
				Complex w(1, 0);
				for(int k = 0; k < i; k++, w = w * wn) {
					Complex x = a[j + k], y = w * a[j + i + k];
					a[j + k] = x + y;
					a[j + i + k] = x - y;
				}
			}
		}
		if(type == -1) for(int i = 0; i < limit; i++) a[i].x /= limit;
	}
	int trans(Complex *a, int n, int type) { int ret = init(n); trans(a, type); return ret; }
};
// 需要先 init 再调用第一个 trans，或者直接调用第二个 trans

NTT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <algorithm>
typedef long long LL;
const int N = /* ... */ + 5; // 2 * (n + m)
template<LL mod, LL g> struct NTT {
	int rev[N];
	int limit;
	int init(int mx) {
		int w = 0;
		limit = 1;
		while(limit <= mx) limit <<= 1, w++; // w = log2(limit)
		for(int i = 0; i < limit; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (w - 1));
		return limit;
	}
	inline LL qpow(LL x, LL y) { LL ret = 1; while(true) { if(y & 1) ret = ret * x % mod; if(!(y >>= 1)) return ret; x = x * x % mod; } }
	inline LL inv(LL x) { return qpow(x, mod - 2); }
	void trans(LL *a, int type) { // type = 1 / -1
		LL invg = inv(g);
		for(int i = 0; i < limit; i++) if(i < rev[i]) std::swap(a[i], a[rev[i]]);
		for(int i = 1; i < limit; i <<= 1) {
			LL wn = qpow(type == -1 ? invg : g, (mod - 1) / (i << 1));
			for(int j = 0; j < limit; j += (i << 1)) {
				LL w = 1;
				for(int k = 0; k < i; k++, w = w * wn % mod) {
					LL x = a[j + k], y = w * a[j + i + k] % mod;
					a[j + k] = (x + y) % mod;
					a[j + i + k] = (x - y + mod) % mod;
				}
			}
		}
		if(type == -1) for(int i = 0; i < limit; i++) (a[i] *= inv(limit)) %= mod;
	}
	int trans(LL *a, int n, int type) { int ret = init(n); trans(a, type); return ret; }
};
// 需要先 init 再调用第一个 trans，或者直接调用第二个 trans

任意模数 NTT（MTT）例题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <cstdio>
#include <algorithm>

typedef long long LL;
const int N = 4e5 + 5;
const LL P1 = 469762049;
const LL P2 = 998244353;
const LL P3 = 1004535809;

template<LL mod, LL g> struct NTT {
	int rev[N];
	int limit;
	int init(int mx) {
		int w = 0;
		limit = 1;
		while(limit <= mx) limit <<= 1, w++; // w = log2(limit)
		for(int i = 0; i < limit; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (w - 1));
		return limit;
	}
	inline LL qpow(LL x, LL y) { LL ret = 1; while(true) { if(y & 1) ret = ret * x % mod; if(!(y >>= 1)) return ret; x = x * x % mod; } }
	inline LL inv(LL x) { return qpow(x, mod - 2); }
	void trans(LL *a, int type) { // type = 1 / -1
		LL invg = inv(g);
		for(int i = 0; i < limit; i++) if(i < rev[i]) std::swap(a[i], a[rev[i]]);
		for(int i = 1; i < limit; i <<= 1) {
			LL wn = qpow(type == -1 ? invg : g, (mod - 1) / (i << 1));
			for(int j = 0; j < limit; j += (i << 1)) {
				LL w = 1;
				for(int k = 0; k < i; k++, w = w * wn % mod) {
					LL x = a[j + k], y = w * a[j + i + k] % mod;
					a[j + k] = (x + y) % mod;
					a[j + i + k] = (x - y + mod) % mod;
				}
			}
		}
		if(type == -1) for(int i = 0; i < limit; i++) (a[i] *= inv(limit)) %= mod;
	}
	int trans(LL *a, int n, int type) { int ret = init(n); trans(a, type); return ret; }
};

LL a[N], b[N], ca[N], cb[N], ans1[N], ans2[N], ans3[N];
int n, m;
LL P;

LL qpow(LL x, LL y, LL mod) { LL ret = 1; while(true) { if(y & 1) ret = ret * x % mod; if(!(y >>= 1)) return ret; x = x * x % mod; } }
LL inv(LL x, LL mod) { return qpow(x, mod - 2, mod); }

NTT<P1, 3> ntt1;
NTT<P2, 3> ntt2;
NTT<P3, 3> ntt3;

int main() {
	scanf("%d%d%lld", &n, &m, &P);
	for(int i = 0; i <= n; i++) scanf("%lld", &a[i]);
	for(int i = 0; i <= m; i++) scanf("%lld", &b[i]);
	int limit = ntt1.init(n + m);
	ntt2.init(n + m), ntt3.init(n + m);
	for(int i = 0; i <= limit; i++) ca[i] = a[i], cb[i] = b[i];
	ntt1.trans(ca, 1), ntt1.trans(cb, 1);
	for(int i = 0; i <= limit; i++) ans1[i] = ca[i] * cb[i] % P1;
	ntt1.trans(ans1, -1);
	for(int i = 0; i <= limit; i++) ca[i] = a[i], cb[i] = b[i];
	ntt2.trans(ca, 1), ntt2.trans(cb, 1);
	for(int i = 0; i <= limit; i++) ans2[i] = ca[i] * cb[i] % P2;
	ntt2.trans(ans2, -1);
	for(int i = 0; i <= limit; i++) ca[i] = a[i], cb[i] = b[i];
	ntt3.trans(ca, 1), ntt3.trans(cb, 1);
	for(int i = 0; i <= limit; i++) ans3[i] = ca[i] * cb[i] % P3;
	ntt3.trans(ans3, -1);
	for(int i = 0; i <= n + m; i++) {
		// 三个质数可以手推 CRT
		// 看着这个推也可以 https://www.cnblogs.com/Memory-of-winter/p/10223844.html
		LL out = 0;
		LL tmp = ans1[i] + (ans2[i] - ans1[i] + P2) % P2 * inv(P1, P2) % P2 * P1;
		out = (tmp + (ans3[i] - tmp % P3 + P3) % P3 * inv(P1 * P2 % P3, P3) % P3 * P1 % P * P2 % P) % P;
		printf("%lld ", out);
	}
	puts("");
	return 0;
}

完结撒花~

参考资料

https://www.cnblogs.com/zwfymqz/p/8244902.html
https://www.bilibili.com/video/BV1Y7411W73U
https://www.luogu.com.cn/problem/solution/P4245
https://www.cnblogs.com/Memory-of-winter/p/10223844.html
https://blog.csdn.net/zhouyuheng2003/article/details/85561887
https://www.cnblogs.com/Sakits/p/8416918.html
https://oi-wiki.org/math/poly/ntt/
https://www.cnblogs.com/zarth/p/7288456.html
http://www.longluo.me/blog/2022/05/01/Number-Theoretic-Transform/